만다라의 신비한 4차원 구조

출처:  http://dongascience.donga.com/news/view/23568

동아 사이언스

만다라는 밀교(密敎)에서 발달한 상징의 형식을 그림으로 나타낸 불화 형식을 뜻한다.

우주의 진리, 만물 이치를 도형화한 것을 일컫는다.  

이번 주 ‘사이언스’ 표지에는 마름모와 사각형, 삼각형 등 3

가지 도형으로만 평면을 빈틈없이 메운 모습이 담겼다.

이는 투과전자현미경(TEM)으로 본 ‘그래핀 준결정’의 모습을 형상화 한 그림이다. 

흡사 깨달음의 경지를 표현한 만다라와 유사한 모습이다.

 

준결정(quasicrystal)은 물질을 이루고 있는 단위 구조가 

규칙적으로 고르게 배열돼 있는 결정과 같은 병진 대칭성은 없지만,

축을 중심으로 회전했을 때 포개지는

회전 대칭성을 갖는 독특한 결정을 말한다.
 
안종열 성균관대 물리학과 교수팀이 이끈 공동 연구팀은

세계 최초로 그래핀 준결정을 만들고,

4개의 독립된 축으로 4차원의 물리적 공간을 구

현하는 데 성공했다고 사이언스 24일자에 발표했다.

그래핀 준결정은 평면 구조의 2차원 물질인

그래핀을 두 층으로 포갠 뒤, 위층을

아래층과 정확히 30도만 어긋나도록 회전시킨 형태다.

따라서 한 층의 x축, y축과

또 다른 한 층의 x‘축, y’축 등 총 4개의 축을 가진 공간이 생긴다.
 
안 교수는 “두 층을 먼저 만든 뒤 한 층을 회전시키는 방식 대신,

실리콘카바이드(SiC) 기판 위에서 애초에 두 층의 각도를 달리해서

그래핀을 성장시키는 ‘에피택시’ 방식을 사용한 덕분에 각도를 정확하게 틀 수 있었다”고 말했다.

그동안 2차원 물질을 기반으로 한 준결정은

이론적으로 제안됐을 뿐, 실험을 통해 입증된 건 이번이 처음이다.

 

그래핀 준결정은 평면 구조의 2차원 물질인

그래핀을 두 층으로 포갠 뒤,

위층을 아래층과 정확히 30도만 어긋나도록 회전시킨 형태다(왼쪽 맨 위).

결정처럼 병진 대칭성을 갖진 않지만

중심축을 기준해 회전 대칭성을 갖는다.

결정과 비슷하게 준결정은 마름모,

삼각형, 사각형 등 3가지 단위 도형만으로

평면을 빈틈없이 채울 수 있다는 특징이 있다. - 자료: 사이언스

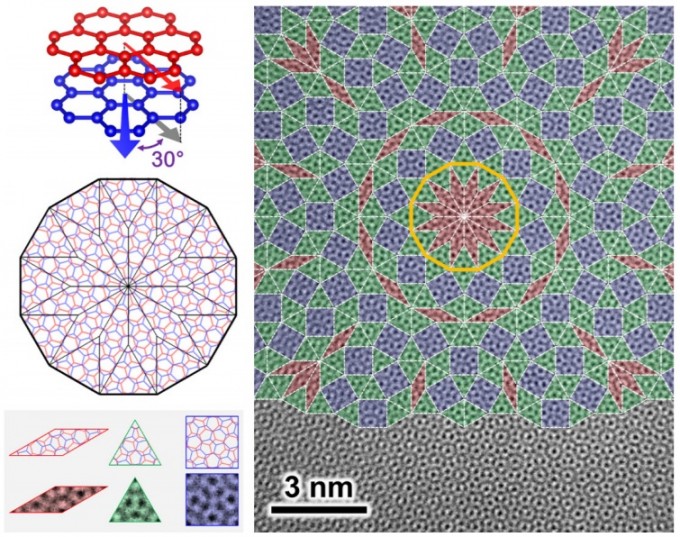
1984년 독일의 물리학자 P. 스탬플리 박사(당시 베를린자유대 교수)는

2차원 물질 두 층을 특정 각도로 포개 준결정 물질을 만들면

4개의 독립적인 차원 축을 구현할 수 있다고 제안했다.

이때 특정 각도는 그래핀처럼 원자가 육각형을

이루고 있는 경우는 30도, 사각형을 이루고 있는 경우는 45도다. 
 
4개의 축을 가진 그래핀 준결정은 4차원 공간에서의

 자기적 특성, 광학 특성, 초전도 현상, 전자구조 현상,

전기적 현상 등 물리 현상을 실험할 수 있는 실험 공간으로 활용할 수 있다.

안 교수는 “우리가 생활하는 공간은 3차원이기 때문에

그동안 4차원의 물리 현상을 이론이 아닌 실험으로

연구하는 것은 불가능한 일로 여겨졌다”며 

“그래핀 준결정을 통해 ‘4차원 공간에서의 물리학 실험’이라는

새로운 연구 분야를 열었다”고 말했다.

이어 그는 “현재 김필립 미국 하버드대 교수팀과 후속 연구를 진행 중”이라고  덧붙였다.
 
앞서 올해 6월 사이언스 온라인판을 통해 처음 공개됐던

이 연구 결과는 이번에 정식으로 출간되면서 표지논문에 선정됐다.