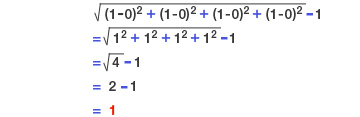< 수학으로 증명하는 4차원의 모습 >
|
4차원 세계는 우리가 실제로 가 보질 않았기 때문에 무슨 일이 벌어질지 모른다. 우리의 경험이 3차원 공간에 갇혀 있기 때문이다. 그런데 아무리 고차원이라고 해도 수학의 확실성과 엄밀성, 자연스러운 확장을 통해 우리는 고차원의 일부를 보고 느낄 수 있다. |

|
|
|

|

|
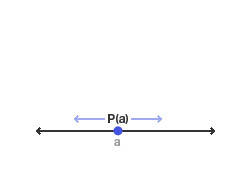
1차원 좌표계 |
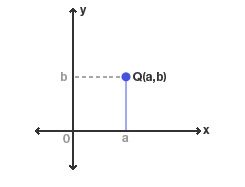
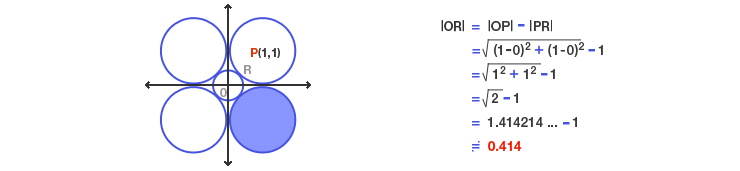
2차원 좌표계 |
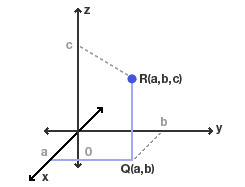
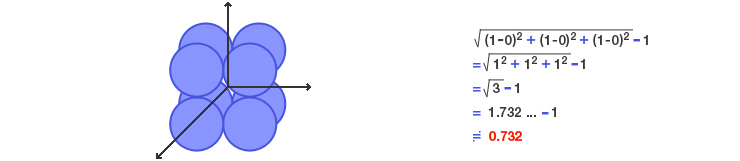
3차원 좌표계 |
|

|
|
|
|

|

|
고차원은 우리가 상상만 할 수 있을 뿐 실제로 가 보질 않았기 때문에 무슨 일이 벌어질지 모른다. 즉, 우리의 생각이 3차원 공간에 있기 때문에 그 보다 높은 차원에서는 어떤 일이 벌어지고 있는지 확인할 수 없다. 그런데 아무리 고차원이라고 해도 수학의 확실성과 엄밀성 그리고 자연스러운 확장에 의하여 우리는 고차원의 일부를 보고 느낄 수 있는 것이다. 그리고 이런 일이 가능한 것은 오직 수학뿐이다.
|
'창작소설 > SF·신비·구도' 카테고리의 다른 글
| 시간여행은 가능한가? (0) | 2011.12.07 |
|---|---|
| 우주에서 느낌을 멈추다 (0) | 2011.12.04 |
| 과학에서 예측하는 다중우주 (0) | 2011.11.06 |
| 아들과의 대화 (0) | 2011.09.29 |
| 다중우주..Multiple Universe (0) | 2011.09.20 |